[Java] Fenwick Tree(Binary Indexed Tree, BIT) - O(lgN)의 부분합 계산

https://www.acmicpc.net/blog/view/21

펜윅 트리 (바이너리 인덱스 트리)

https://www.acmicpc.net/problem/2042

2042번: 구간 합 구하기

 

 

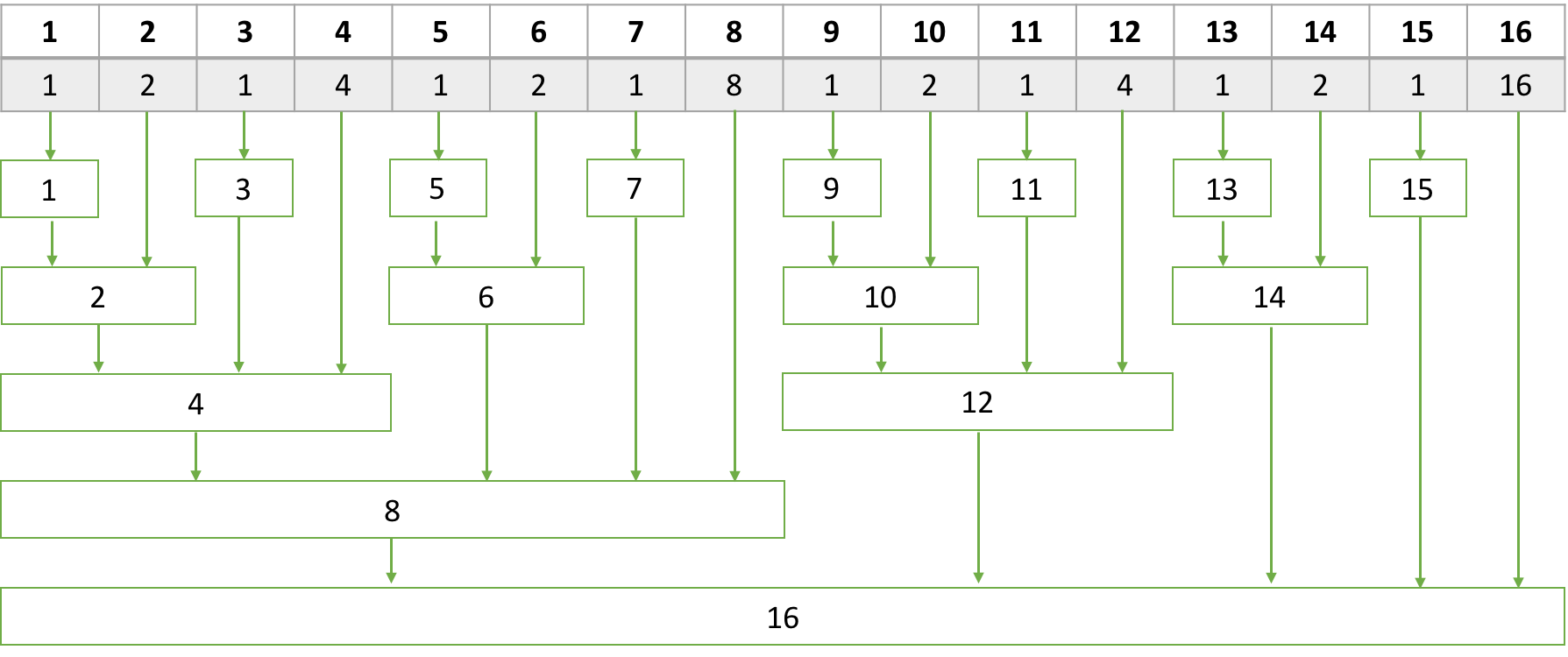
update는 index가 포함된 모든 tree에 대하여 => i += (i & -i)

sum은 i -= (i & -i) 에 대하여

 

* (i & -i) 는 i를 이진수로 나타냈을 때 가장 우측에 나오는 1이 나타내는 수를 의미

=> tree[i]는 (i & -i) 개의 칸에 대한 정보를 담고 있다.

 

 

import java.util.*;
import java.io.*;

public class g1_2042{
    static FastScanner fs = new FastScanner();
    static PrintWriter pw = new PrintWriter(System.out);

    static int n, m, k;
    static long[] tree, pp;
    public static void main(String[] args){
        n = fs.nextInt();
        m = fs.nextInt();
        k = fs.nextInt();

        pp = new long[n + 1];
        // 해당 칸의 원래 값
        tree = new long[n + 1];
        // 해당 index까지 (i&-i)개의 칸의 합

        for (int i=1;i<=n;i++){
            pp[i] = fs.nextLong();
            update(i, pp[i]);
        }

        for (int t=0;t<m+k;t++){
            if (fs.nextInt() == 1){
                int index = fs.nextInt();
                long num = fs.nextLong();
                update(index, num - pp[index]);
                pp[index] = num;
            }
            else{
                int left = fs.nextInt();
                int right = fs.nextInt();
                pw.println(sum(right) - sum(left - 1));
            }
        }
        pw.close();
    }

    static void update(int i, long num){
        while (i <= n){
            tree[i] += num;
            i += (i & -i);
        }
    }

    static long sum(int i){
        long ans = 0;
        while (i > 0){
            ans += tree[i];
            i -= (i & -i);
        }
        return ans;
    }

//    ----------input function----------

    static void sort(int[] a){
        ArrayList<Integer> L = new ArrayList<>();
        for (int i : a) L.add(i);
        Collections.sort(L);
        for (int i = 0; i < a.length; i++) a[i] = L.get(i);
    }

    static class FastScanner{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer("");
        String next(){
            while (!st.hasMoreTokens()){
                try{
                    st = new StringTokenizer(br.readLine());
                }catch (IOException e){
                    e.printStackTrace();
                }
            }
            return st.nextToken();
        }

        int nextInt(){
            return Integer.parseInt(next());
        }

        int[] readArray(int n){
            int[] a = new int[n];
            for (int i = 0; i < n; i++) a[i] = nextInt();
            return a;
        }

        long nextLong(){
            return Long.parseLong(next());
        }
    }
}